E Momentum Compaction Example

Consider a particle of momentum \(p_0\) circulating in a uniform bend field of strength \(B\) with radius \(R_0 = p_0/eB\). In the same field, relative to this orbit and concentric to it, a particle of momentum \(p\) would circulate with a radius \(R = R_0(p/p_0) \equiv R_0(1+\delta)\), where \(\delta = \Delta p/p_0 = (p-p_0)/p_0\).

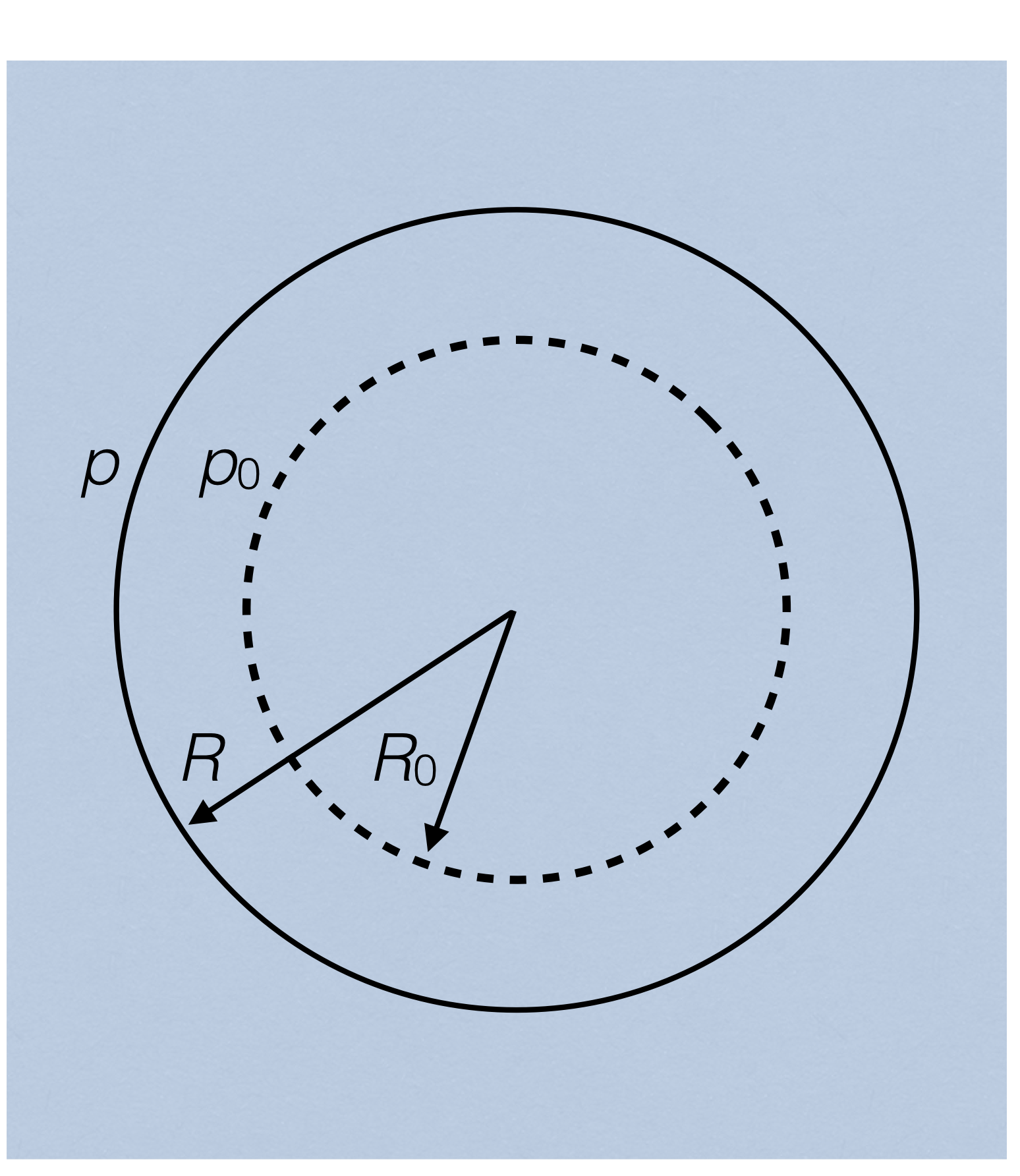
We would say that the dispersion function of this arrangement has value \(D=R_0\) since the difference between the orbits is \(\Delta x = R-R_0 = R_0\delta \equiv D\delta\).

Now take the circle and slice it along a diameter. Separate the two halves with a drift space (where \(B=0\)) of distance \(d\) to form a “racetrack” configuration. The original momentum particle will now travel on a path that has total circumference \[ C_0 = 2\pi R_0 + 2d \] while the second particle will travel along a path with \[ C = 2\pi R + 2d = 2\pi R_0 (1+\delta)+2d \]

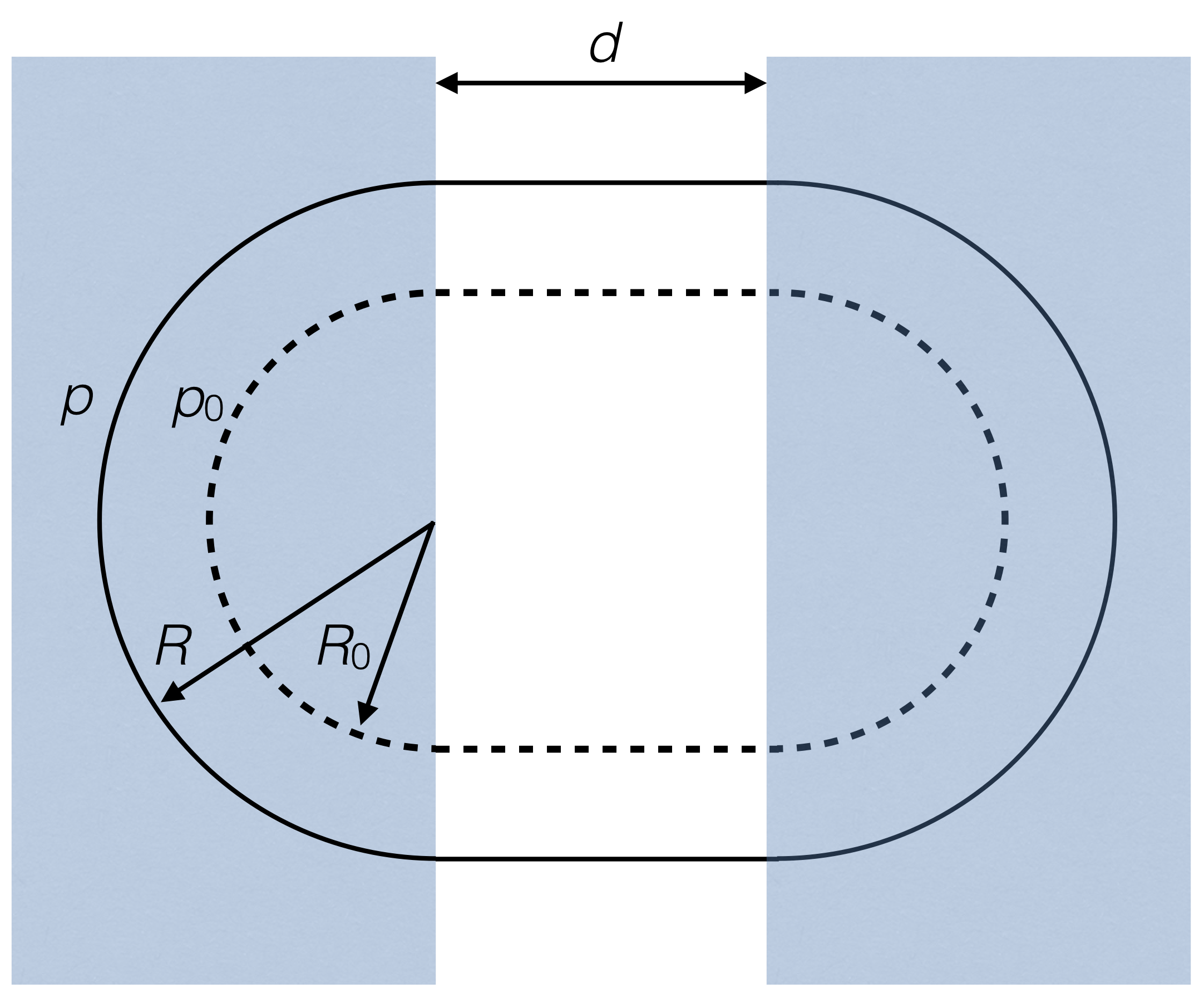
Note that for this case, the dispersion function is still \(D=R_0\) everywhere.

Now, examine the time it takes each particle to go around its respective orbit: \[ T_0 = \frac{C_0}{v_0} = \frac{2\pi R_0+2d}{v_0} \] and \[ T = \frac{C}{v} = \frac{2\pi R_0(1+\delta)+2d}{v} \] The time difference is then \[ \Delta T = T-T_0 =(2\pi R_0+2d) (1/v-1/v_0) + (2\pi R_0/v)\delta \] from which \[ \frac{\Delta T}{T_0} = (\frac{v_0}{v}-1) + \frac{2\pi R_0}{2\pi R_0+2d}\cdot\frac{v_0}{v}\cdot\delta \\ =(\frac{1}{1+\Delta v/v_0}-1) \\ + \frac{2\pi R_0}{2\pi R_0+2d}\cdot\frac{1}{1+\Delta v/v_0}\cdot\delta \\ \approx -\frac{\Delta v}{v_0} + \frac{1}{1+d/\pi R_0}\frac{\Delta p}{p} \] or, \[ \frac{\Delta T}{T_0} = \left( \frac{1}{1+d/\pi R_0} - \frac{\Delta v/v_0}{\Delta p/p_0}\right) \frac{\Delta p}{p_0}. \] Note that from \(\gamma \equiv 1/\sqrt{1-\beta^2}\) and \(p=mc\beta\gamma\), \[ \frac{dv}{v} = \frac{1}{\gamma^2}\frac{dp}{p} \] so that \[ \frac{\Delta T}{T_0} = \left( \frac{1}{1+d/\pi R_0} - \frac{1}{\gamma^2}\right) \frac{\Delta p}{p_0}. \] The first term in the parentheses is called the momentum compaction factor, \(\alpha_p\). (Yes, another alpha!) We saw in the homework that \[ \alpha_p = \langle \frac{D}{\rho}\rangle. \] In our example, \(D = R_0 = \rho\), but the average is taken over the circumference: \[ \langle \frac{D}{\rho}\rangle = \frac{1}{C_0}\int_0^{C_0} \frac{D}{\rho} ds = \frac{1}{2\pi R_0+2d}\int_0^{C_0}\frac{D}{R_0(s)}ds\\ = \frac{1}{2\pi R_0+2d}\int_0^{2\pi R_0}\frac{R_0}{R_0}ds = \frac{2\pi R_0}{2\pi R_0+2d}\\ = \frac{1}{1+d/\pi R_0} ~~~~~~~~~ \checkmark \] The total quantity in the parentheses, is known as the slip factor, \(\eta\), \[ \eta \equiv \alpha_p - \frac{1}{\gamma^2}. \]

In summary, the slip factor tells us how much more time, relative to the ideal circulation time, it will take a particle of momentum deviation \(\Delta p/p_0\) to circulate the ring. Part of this is due to the fact that it has higher velocity (second term), while the first term shows us that path length differences also play a role. This first term – the momentum compaction factor – is determined by the ratio of the periodic dispersion function to the local bending radius averaged over the complete circumference. Note that while \(D(s)\) may be non-zero in the straight sections of the ring, only the dispersion in the bending magnets will contribute to the integration.

And finally, there will be an energy (i.e., \(\gamma\)) where the slip factor will be zero, namely, \(\gamma = \gamma_t \equiv 1/\sqrt{\alpha_p}\). This transition energy (transition \(\gamma\)) in our example would be \[ \gamma_t = \sqrt{1+d/\pi R_0} \]

A real storage ring of course can have many bend and drift regions and will require additional focusing elements, and so the dispersion function of the ring – hence \(\alpha_p\), \(\gamma_t\) and \(\eta\) – can be tailored by the accelerator designer to meet the overall needs of the device.